Was ist „Rechnen“
Unter Rechnen versteht man allgemein den Umgang mit Zahlen mit mehr oder weniger komplizierten Regeln (Mathematik). Man kann auch damit rechnen, dass am nächsten Morgen gutes Wetter zu erwarten ist. Dies gehört aber eher in das Gebiet der Spekulationen, es sei denn man hat mit einer riesigen Anzahl an Zahlen, die für die Bestimmung des Wetters wichtig sind, gerechnet und sieht mit einer gewissen Sicherheit eine Wahrscheinlichkeit voraus. Andere wiederum rechnen mit etwas ab und haben gelegentlich dabei auch etwas berechnet.
Vom Beginn des Rechnen
Der Mensch begann zu zählen, mit den Fingern, Kerben und Gegenständen. Die nächst höhere Form des Zählens war das Messen. Es entstanden die ersten Rechengänge, die über das Addieren und Multiplizieren hinaus gingen. In den fruchtbaren Überschwemmungsgebieten der großen Flüsse (Euphrat, Tigris, Nil) mussten die Besitztümer definiert werden. Zur Flächenbestimmung waren Fachleute eingesetzt, die in Amt und Würde den hohen Priestern gleich kamen.

Rechnen und Messen vor 3400 Jahren
Einfache Formen des Rechnens
Es gibt ganz einfache Beispiele aus dem Gebiet der Algebra, bei denen es keine Spekulationen oder Zweifelsfälle gibt. Die Summe aus zwei Zahlen ergibt eine Ergebnis ohne Alternativen (2 + 3 = 5). So ergeht es allen Grundrechenarten und auch den aufwendigeren Methoden. Man kann die Probe mit Steinen oder anderen geeigneten Gegenständen machen.
In der Geometrie ist es ebenso. Die Gesetze über Dreiecke, Flächenberechnungen, Umfang des Kreises bzw. Bestimmung der Zahl p und unendlich viele andere Beispiele sind bekannt.
Aus dem Mathematikunterricht kennt man die Umkehrung der einfachen Rechenaufgaben. Es wird nicht abgefragt, wie viel ist die Summe aus zwei Zahlen, sondern das Problem wird verkleidet und man erzählt von Bauern, die soundsoviel Pfund Kartoffeln aufteilen usw. und man muss sich die Rechenaufgabe selber formulieren.
Geschichte und Anwendung des Rechnens (insbesondere im Bauwesen)
In der Naturwissenschaft entwickelten sich Rechenmodelle, mit denen Erscheinungen beschrieben und hergeleitet werden. Als sich Galileo-
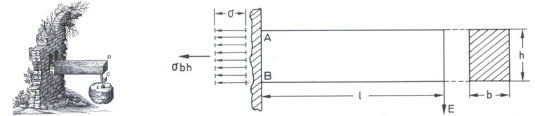
Das Verhalten eines verbogenen Holzbalkens untersuchte er auch, kam aber noch nicht auf das richtige Ergebnis. Erst 190 Jahre später wurde das bei Baufachleuten bekannte Widerstandsmoment mit dem Wert b×h²/6 eindeutig durch Navier bestimmt, mit dem die Zugspannung in einem rechteckigen Querschnitt eindeutig berechnet werden kann. Die Richtigkeit der Formel kann an Versuchen überprüft werden.
Galileo-Galilei und der gebogene Balken, 1638
Im 18. Jahrhundert haben das erste Mal Mathematiker (Thomas le Seur, Francois Jacquier und Ruggero Giuseppe Boscovich) statische Untersuchungen an der Peterskuppel in Rom angestellt und sich ausführlich bei den Fachleuten aus der Bauwelt entschuldigt, dass sie sich mit der trockenen Materie der Mathematik an ein Bauwerk wagten. Das Ergebnis der Untersuchung war die genaue Angabe einer Zugkraft, mit der die Kuppel auseinandergezogen wird (es waren bedrohliche Risse entstanden) und der Vorschlag, mit welchen Maßnahmen der Kraft entgegen gehalten werden kann.
Über dieses Ergebnis wurde schon kräftig gestritten. Es gab Wortmeldungen, die Baukunst hätte schon seit Tausenden von Jahren keine mathematischen Hilfestellungen nötig gehabt bis zu dem Vorwurf, eine allzu theoretische Herangehensweise an ein Bauwerk würde diesem schaden oder dieses verschandeln (eine Ideologie, die bis in die Anfänge des 20. Jahrhunderts heftig weiter leben konnte, als man riesigen und höchst sachlich erscheinenden von Ingenieuren berechneten Tragwerken aus Eisen burgähnliche Steingebäude voran setzte – Brücke über den Rhein bei Worms, diverse Hauptbahnhöfe usw.).

Conway-
Wahrheitsgehalt des Rechnens
Bei den einfachen Formen des Rechnens wird die Wahrheit nicht angezweifelt, vorausgesetzt man hat sich nicht verrechnet.
Eine besondere Form ist die Beschreibung und Berechnung von virtuellen Vorgängen. Man kann einen Körper in Gedanken zerschneiden (was in der Wirklichkeit nicht geschehen soll) und berechnet an der Schnittstelle die Kräfte, die vor dem Schnitt in dem Körper herrschten, indem man sich kleine zerrissene Fasern, gedrückte oder gezogene Moleküle, ersatzweise anmontierte Federn oder kleine Männchen vorstellt, die die Kräfte übernehmen. Der Statiker spricht von der „Ermittlung der inneren Schnittkräfte“. Anhand der errechneten inneren Kräfte können Spannungen ermittelt, diese mit zulässigen Spannungen verglichen werden und mit speziellen Sicherheitstheorien (zu welchem Anteil will man in der Wirklichkeit unter dem Bruchzustand bleiben) ist man in der Lage, das Verhalten eines Bauteils vorherzusehen, um sich vor Schaden zu schützen.
Eine andere begeisternde Form der Berechnung: niemand kann den Mond auf eine Waage stellen und trotzdem ist sein Gewicht bekannt. Aus dem Gesetz der Anziehungskraft der Massen müsste der Mond auf die Erde fallen; durch die Zentrifugalkraft seiner Drehbewegung müsste er ins All geschleudert werden. Aus dem Gleichgewicht der Kräfte bzw. Bewegungen kann man die Masse des Mondes berechnen (kleine Ungenauigkeiten beim Vermischen der Begriffe Gewicht, Masse und Kräfte sind an dieser Stelle zu entschuldigen).
Rechnen in der Naturwissenschaft
Bei allen soeben erwähnten Prozessen und Theorien bewegt man sich auf dem Gebiet der Naturwissenschaften. Man untersucht und versucht Vorgänge zu erklären, die sich ohne den Menschen abspielen. Deshalb kann man sie objektiv beobachten und beurteilen. Zur Bestimmung von Gesetzmäßigkeiten werden Rechenmodelle entwickelt. Die Modelle sind nicht mit der Wirklichkeit identisch, sondern beschreiben sie möglichst genau.
Wie eine Theorie lange Zeit „richtig“ sein kann und plötzlich ungültig wird, aber weiterhin im praktischen Leben sinnvoll weiter leben kann, zeigt ein Beispiel aus den Anfängen der Elektrotechnik. Man war lange Zeit der Überzeugung, der Strom würde von einem Pol zum anderen fließen und konnte dank dieser Theorie Gleichstrommotoren und ähnliche Geräte entwerfen und konstruieren. Sie arbeiteten entsprechend der Theorie. Später wurde erkannt, dass der Strom genau anders herum fließt. So lebten eine lange Zeit der technische Strom und der physikalische Strom nebeneinander, weil die Geräte mit ihren Bezeichnungen (Polangaben etc.) nicht von heute auf morgen umgerüstet werden konnten, man in der Theorie aber schon nach neuen Erkenntnissen handelte.
Einen Dämpfer erlebten die Naturwissenschaften, als von Einstein bewiesen wurde, dass die bis dahin entwickelten Modelle und Ansichten und Vorstellungen von der uns umgebenden materiellen Welt gar nicht so absolut sondern sehr relativ sind. An dieser Stelle soll auf dieses komplexe Thema nicht eingegangen werden.
Rechnen in Gesellschaftswissenschaften
Viele sprechen auch von den Geisteswissenschaften – das ist Ansichtssache, ob ein Geist wissenschaftlich behandelt werden kann. Der Autor überlässt es anderen, sich damit näher zu beschäftigen.
Versuche, Prozesse im menschlichen Zusammenleben zu berechnen, haben eine wesentliche Fehlerquelle. Das Objekt der Betrachtung – der Mensch mit seinen Beziehungen – ist gleichzeitig auch Subjekt der Betrachtung. Einfach ausgedrückt: die Einordnung des Betrachters in seiner gesellschaftlichen Umgebung beeinflusst die Fähigkeit und die Qualität der Beobachtung. Begriffe und Zustände wie Sein und Bewusstsein sind nicht mathematisch zu analysieren. Hier wird auf die philosophischen Auseinandersetzungen der letzten Jahrtausende verwiesen. Z.B. „das Sein beeinflusst das Bewusstsein“.
Rechnen in der Praxis (in der technischen)
In der Praxis hat sich ein großes Feld für Berechnungen eröffnet, insbesondere seit der mühsame Weg der einfachen Rechenoperationen durch die Maschine ersetzt wurde. Alles, was irgend wie in Zahlen gefasst werden kann, wird berechnet. Das Ergebnis ist nicht unbedingt besser geworden. Oft gilt das Gegenteil.
Noch vor dreißig Jahren gehörte zum Erscheinungsbild eines Ingenieurs ein Rechenschieber. Dieses Instrument ersparte einem mühsame Multiplikationen. Das Ergebnis aber hatte nur relative Gültigkeit, weil es nur aus übersichtlichen Zahlen bestand – mehrere Stellen hinter dem Komma kamen nicht vor – und der Ingenieur musste die Dimension der Zahl selber bestimmen oder überschlagen. Die Zahlenfolge 123 kann 1,23 oder 12,3 oder 123 usw. bedeuten. Hierdurch wurde u.a. ein konstruktives Verständnis gefördert und auch die Fähigkeit, ein Ergebnis auf Plausibilität zu überprüfen bzw. das Rechenwerk mit der Wirklichkeit zu vergleichen.

Der Rechenschieber
Ein einfaches und anschauliches aber nicht dramatisches Beispiel für die Entwicklung von einfachen Operationen zu einem wahren Formelwerk ist die Bestimmung der zulässigen Anzahl an Bewehrungsstäben in einem Betonquerschnitt. Damit die Bewehrungsstäbe Kräfte auf den Beton übertragen können, müssen sie von Beton umwickelt sein. Man stellte fest, dass der Zwischenraum von einem Stab zum nächsten mindestens dem Stabquerschnitt entsprechen muss. Dann gibt es Bügel, um die Bewehrungsstäbe zu fixieren und einen Mindestabstand dieser Bügel zum äußeren Rand des Querschnitts. In der einfachen Version kennt man eine Tabelle, in der in der ersten Spalte die Stabquerschnitte eingetragen sind, in der ersten Zeile mögliche Balkenbreiten und im Kreuzungspunkt zwischen herausgesuchter Zeile und Spalte kann man die Anzahl der maximal zulässigen Stäbe ablesen. In neuer Form wird dies anhand einer Formel berechnet:

Immerhin ist das Zahlenwerk real, wenn es auch höchst unübersichtlich erscheint. Es kommt eine konkrete Zahl heraus. Die Formel und die einfachere Tabelle gehören aber nicht mehr zu den exakten Berechnungen der Naturwissenschaften. Der Mensch hat einen Parameter dazu erfunden (Parameter nach Duden: „konstante oder unbestimmt gelassene Hilfsvariable“ – also eine Art Hilfsgriff): den zulässigen Mindestabstand zwischen den Stäben. In einer genauen Berechnung müssten die Mindestabstände aus den Kräften hergeleitet werden, die bei der Verbundwirkung zwischen Stahl und Beton entstehen. Ein endloses Unterfangen und man könnte sagen, man kommt vom Hundertsten ins Tausendste. Aus dieser Perspektive sind einfache Tabelle und komplizierte Formel gleichermaßen ungenau, wobei die Formel vortäuschen könnte, sie sei weniger ungenau, was sich aber als Unsinn erweist.
Technische Vorgänge sind sehr komplex, obwohl sie als einfacher erscheinen als biologische oder biochemische Vorgänge. Für ein Berechnungsmodell zu Erklärung oder planerischen Vorausbestimmung der Vorgänge (oder Nicht-
Viele Beispiele
In der Bauwelt begegnet man ständig Beispielen mit Berechnungsmodellen, um einfache Zusammenhänge zu berechnen. Man spricht auch von „bautechnischen Nachweisen“ und liest in der Anforderung der Baubehörde Begriffe wie: Berechnung des Schallschutzes, Berechnung des Wärmeschutzes (oder des Energieverbrauchs), Berechnung der Versickerungsfläche von Regenwasser, Berechnung der Stellplätze, Berechnung der Ausnutzung der Grundstücksfläche, Berechnung der Abstandsflächen, Berechnung der naturrechtlichen Ausgleichsflächen (dabei berechnet man den Ökowert von Pflanzen) usw. usf.
Schallschutz: Bei einem Doppelhaus stellt man die gemeinsame Trennwand aus zwei Mauern her mit einer dazwischen liegenden Dämmschicht. Man sieht auch vielseitige Berechnungen mit Berücksichtigung der Eigengewichte der einzelnen Bauteile in den Wohngebäuden, bei denen das gleiche Ergebnis heraus kommt. Dass durch Mörtelstücke, die sich beim Aufmauern in die Dämmung gedrückt haben, der ganze Schutz hinfällig wird, steht in keiner Berechnung.
Wärmeschutz: Ein Einfamilienhaus mit modernen Dämmsteinen und einem normalen Flächenanteil der Fenster erfüllt mit Leichtigkeit die Anforderungen an einen Wärmeschutz. Dennoch sieht man seitenlange Berechnungen mit Tabellen, in denen sogar der wöchentliche Energieverbrauch vorgerechnet wird. Man kann auch theoretisch ein großes offenes Loch in einer Außenwand lassen und den Rest der Wand so dick dämmen, dass rechnerisch ein hoch gedämmter Raum entsteht.
Versickerungsfläche von Regenwasser: Regenwasser kann ohne Kanalisation in des Grundwasser eingeführt werden, in manchen Gebieten ist dies sogar Vorschrift. Es versickert. Damit es keine Überschwemmungen gibt, bevor das Wasser versickert ist, muss man einfach ausgedrückt berechnen, wie schnell Wasser in einem Boden aufgenommen werden kann. Diese Fähigkeit des Bodens hängt von vielen Parametern ab, die nie eindeutig zu bestimmen sind. Folglich gibt es viele Kennwerte, die in eine Formel eingearbeitet wurden. Der Verfasser hat einmal an einem konkreten Beispiel nachgewiesen, wie bei geringfügiger Änderung der Kennwerte riesengroße Veränderungen des Ergebnisses heraus kamen. Das Ergebnis ist willkürlich bzw. abhängig von der Fähigkeit des Aufstellers der Berechnung, verschiedenste Faktoren kunstvoll zu kombinieren.
Die Beispielliste kann endlos fortgesetzt werden.
Rückwärts rechnen
Da in vielen Rechnungsmethoden Kennwerte eingeführt werden, kann man in so genannten „rechnerischen Nachweisen“ vom erwünschten Ergebnis ausgehend großzügig manipulieren. Vom Ergebnis wird rückwärts gerechnet. Weil heutzutage die Nachweise mit Rechenprogrammen erstellt werden, ist eine mehrfacher Durchgang der Rechenoperation kein zeitliches Problem mehr. Diese Vorgehensweise ist aus Sicht der Erfinder der jeweiligen Formel zwar verwerflich, aber tägliche Praxis.
Reale und erfundene Berechnungsmethoden
Unabhängig vom Wahrheitsgehalt vieler Berechnungsmethoden kann man zwei Gruppen beschreiben:
Die realen Berechnungsmethoden versuchen, Vorgänge in der Natur oder Umwelt – physikalische und chemische – möglichst genau zu beschreiben und Gesetzmäßigkeiten der Zusammenhänge zu definieren. Die einzelnen Vorgänge existieren ohne den Erfindungsgeist des Menschen. Körper ziehen sich gegenseitig an; deshalb gibt es die Gesetze der Statik. Wärme fließt immer zum Kalten, langsam oder schnell; dafür gibt es naturwissenschaftliche Gesetze.
Erfundene Berechnungsmethoden beschreiben Vorgänge oder Zustände, die ohne die Existenz des Menschen nicht vorhanden waren. Der Mensch versucht seine eigenen Regeln des Zusammenlebens in manchen Bereichen in rechnerische Abhängigkeiten zu formen. Beispielsweise im Baurecht werden so genannte Abstandsflächen definiert, die nach bestimmten Regeln berechnet werden. Auf den berechneten Abstandsflächen dürfen keine anderen Gebäude stehen, es sei denn man findet Ausnahmeregelungen. D.h. die Flächen bestehen nur durch die Erfindungsgabe des Menschen und nur dort, wo ein gesellschaftliches System dies bestimmt. Dennoch wird manches Mal sehr verbissen an den Abstandsflächen gerechnet.
Ein Überblick beschränkt sich auf das Gebiet des Bauwesens, wo sich der Verfasser am besten auskennt. In anderen Bereichen (s. Rechnen in Gesellschaftswissenschaften) gibt es fast nur Modelle aus der Familie der erfundenen Berechnungen. Hierbei weicht die berechnete Welt oft von der wirklichen Welt ab, wie man bei Wirtschaftsprognosen immer wieder feststellen kann. Man kann nicht so eindeutig Prozesse vorberechnen, wie es bei den Naturwissenschaften möglich ist.